model的分類

一言以蔽之：模型有三類——analytical、numerical、table-lookup。

在上期文章中，我們介紹了BSIM3內，carrier mobility、threshold voltage、saturation current這三個MOSFET特性的模型，可以發現模型的建立一開始大多是假設一些理想的狀況，利用物理計算出來，這類推導出來的模型叫做「analytical model」。

然而真實世界上沒有這麼理想的狀況，而是有一些「boundary condition」，於是研究人員就會在滿足邊界條件下去對原模型加入一些修正項，有些參數是實驗得來、有些參數是fitting parameter，模型就變成了「numerical model」。

有些時候，連fitting也搞不定的時候，寫不出一個漂亮的連續性函數，就乾脆用查表法，模型就變成了「table-lookup model」。

下面用一個簡單的例子，來說明這三種model的差異。

這是一個彈簧，它的彈簧受力F和彈簧伸長量x的量測結果如下表：

analytical model

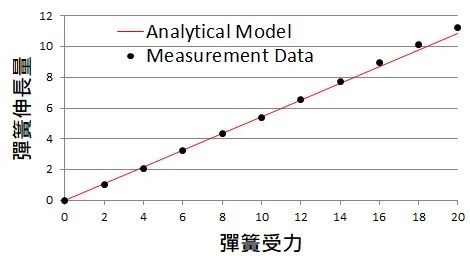
我們都讀過虎克定律，說彈簧伸長量x跟彈簧受力F成正比，所以analytical model就是F=k*x，k是常數。

將上表的資料代入，我們大概可以估計出k=1.84，於是就得到模型F=1.84*x。若受力F=17，代入此模型，可得到伸長量x=9.24。

這個模型和實驗量測數據的作圖如下。

numerical model

從上面那個圖可以看出，analytical model的準度還可以，但不太夠準，尤其是在受力大的時候，我們發現彈簧的伸長量會變大一些。於是，我們就改一下模型，變成F=k*x^v，其中v略小於1。

將上表的資料代入，我們大概可以估計出k=2.00、v=0.95，於是就得到模型F=2.00*x^0.95。若受力F=17，代入此模型，可得到伸長量x=9.51。

這個模型和實驗量測數據的作圖如下，可以發現比純物理模型更準確。

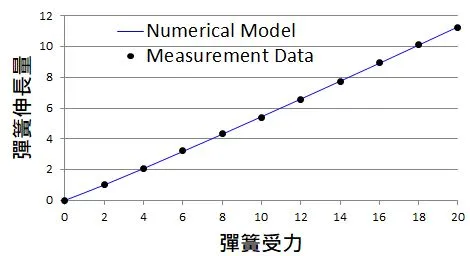
table-lookup model

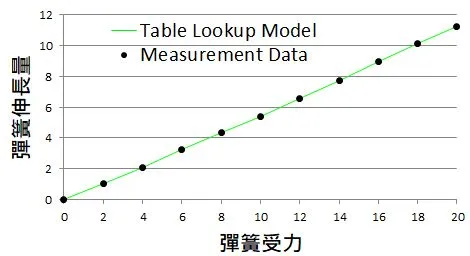
那如果我們無法想出F=k*x^v這種模型怎麼辦，就可以用lookup table，最簡單的查表法就是相鄰二點的內插。

若受力F=17，代入此模型，可得到伸長量x=(8.93+10.11)/2=9.52。

這個模型和實驗量測數據的作圖如下。