一言以蔽之:鬼腳圖是一種不公平的抽籤方式。
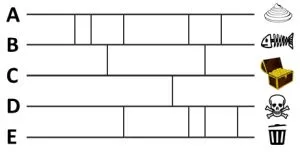
鬼腳圖,又稱為爬梯圖,就是看有幾個人要抽籤,就先畫幾條平行線,再於相鄰的平行線間任意畫幾條垂直的線。以一端為起點,另一端為終點,每個人選一個起點,走到終點就是抽中的項目。
在餐廳等上菜,小朋友不耐煩的時候,我就會拿這個遊戲出來玩,因為只需要原子筆在餐巾紙(克難一點衛生紙也可以)上畫一畫就可以了,道具隨手可得,而且還可以讓小朋友畫垂直的線,他們也會很有參與感。玩完以後,還可以解釋一下背後的原理。
問題一:每支籤都一定會有人抽中嗎?
是的,無論圖怎麼畫(只要滿足規則地畫、不要有交錯的線),鬼腳圖一定都是1-to-1 mapping。
先考慮一開始沒有垂直線的時候,本來就是一對一,後來每加入一條垂直線,都是那二條平行線的選項交換而已,所以最後還是一對一。
問題二:每種排列組合都會出現嗎?
這題的答案也是肯定的,也就是說,每個人都可能抽中所有的選項之一。
只要多畫幾條垂直線,多交換幾次,就可以排出所有想要的可能。
問題三:這個抽籤是公平的嗎?
答案是否定的,這也許就不跟小朋友解釋了,因為解釋完以後,下次就不能作弊了(笑)。
先考慮一開始沒有垂直線的時候,寶箱一定是C的。假設只加上一條垂直線,這條無論是加在AB之間、還是DE之間,寶箱還是C的。就算可以加上多條垂直線,但如果這些垂直線總是在畫在BC之間,不管畫幾條垂直線,寶箱總是B或C才能拿到。
現在有五個人要抽籤,所以有五條平行線,我寫了個程式模擬一下,在不同數量的垂直線下,來統計最後位子的機率,結果附在最後。
這個模擬結果顯示:
- 不管垂直線有幾條,停留在原來的位子的機率總是最高,次高的機率是移動到隔壁位子,移動到越遠位子的機率越低。
- 隨著垂直線數量的增加,機率會越來越平均。
因此在這個遊戲中,當寶箱在位子三,選擇C總是對的,而且還要主張少畫幾條垂直線,來維持你的優勢。那如果寶箱在位子一,而你剛好又是距離最遠的E,那就要主張多畫幾條垂直線,來平衡你的劣勢。
| 隨機畫4條垂直線 | 位子1 | 位子2 | 位子3 | 位子4 | 位子5 |
| A | 49% | 33% | 14% | 4% | 0% |
| B | 33% | 30% | 22% | 11% | 4% |
| C | 14% | 22% | 27% | 22% | 14% |
| D | 4% | 11% | 22% | 31% | 33% |
| E | 0% | 4% | 14% | 33% | 49% |
| 隨機畫8條垂直線 | 位子1 | 位子2 | 位子3 | 位子4 | 位子5 |
| A | 37% | 30% | 19% | 10% | 5% |
| B | 29% | 26% | 20% | 14% | 10% |
| C | 19% | 20% | 21% | 20% | 19% |
| D | 10% | 14% | 20% | 26% | 29% |
| E | 5% | 10% | 19% | 30% | 37% |
| 隨機畫12條垂直線 | 位子1 | 位子2 | 位子3 | 位子4 | 位子5 |
| A | 31% | 27% | 20% | 13% | 9% |
| B | 27% | 24% | 20% | 16% | 13% |
| C | 20% | 20% | 20% | 20% | 20% |
| D | 13% | 16% | 20% | 24% | 27% |
| E | 9% | 13% | 20% | 27% | 31% |
| 隨機畫32條垂直線 | 位子1 | 位子2 | 位子3 | 位子4 | 位子5 |
| A | 22% | 21% | 20% | 19% | 18% |
| B | 21% | 21% | 20% | 19% | 19% |
| C | 20% | 20% | 20% | 20% | 20% |
| D | 19% | 19% | 20% | 21% | 21% |
| E | 18% | 19% | 20% | 21% | 22% |