一言以蔽之:SAR ADC是一種常見的類比數位轉換器。
前文提到管線式和三角積分式類比數位轉換器,這次來說說第三種常見的ADC——SAR ADC。
假設我們穿越回去古代沒有計算機的時候,需要計算根號2的答案,我們可以使用中學所學的「二分逼近法」。
1²=1、2²=4,所以1≤√2≤2 1²=1、(3/2)²=2.25,所以1≤√2≤3/2 (5/4)²≈1.56、(3/2)²=2.25,所以5/4≤√2≤3/2 (11/8)²≈1.89、(3/2)²≈2.25,所以11/8≤√2≤3/2 (11/8)²≈1.89、(23/16)²≈2.07,所以11/8≤√2≤23/16 (45/32)²≈1.98、(23/16)²≈2.07,所以45/32≤√2≤23/16 (45/32)²≈1.98、(91/64)²≈2.02,所以45/32≤√2≤91/64 算到這裡差不多了,就取(45/32)和(91/64)的平均吧,得到√2≈181/128=1.4140625
SAR ADC的全名是Successive-Approximation Register ADC,其實也是用binary search來量化輸入訊號。
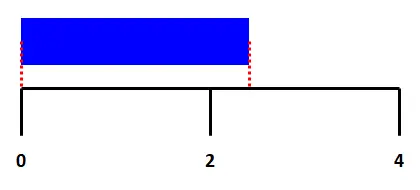
拿一把總長度為4cm的直尺,來量測一條藍色緞帶的長度。先將直尺放在緞帶下方,發現緞帶超過直尺的中間,表示緞帶長度在2cm~4cm之間。
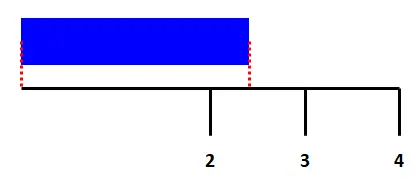
接著看右半邊,發現緞帶沒有超過一半,表示緞帶長度在2cm~3cm之間。
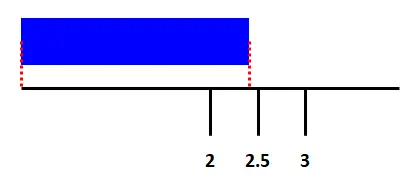
接著看2cm~3cm,發現緞帶沒有超過一半,表示緞帶長度在2cm~2.5cm之間。
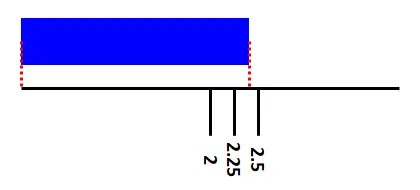
接著看2cm~2.5cm,發現緞帶超過了一半,表示緞帶長度在2.25cm~2.5cm之間。
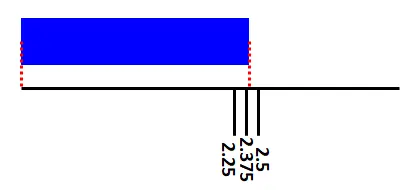
最後看2.25cm~2.5cm,發現緞帶超過了一半,表示緞帶長度在2.375cm~2.5cm之間,我們可以拿(2.375+2.5)/2=2.4375cm作為緞帶長度的測量值。
這方法的好處,就是不用整把直尺都畫上細細的刻度,只需要在必須的地方畫刻度即可。另外一個優點是,二分逼近的查找,相對於十分逼近的比較次數會少得多。