一言以蔽之:在立體空間中用相同球體所形成的最密堆積,密度可高達74%。
克卜勒猜想
老闆在中秋節送了員工每人一箱水果,箱子很大很美觀,但裡面防撞的報紙不少,裝的水果倒是沒幾顆(沒辦法,這二年的通貨膨脹太嚴重了),於是我們玩起了遊戲,把數箱的棗子合併擠進盡可能少的箱子內。
如果把每一顆水果都當成一樣大的球,那這個問題等效就是「在三維空間中,要如何排列出最多的球體」,像這種知名的問題,早就有人探索過了。十七世紀發表行星三大運動定律的克卜勒,他猜這題的答案是:最多可以塞到全部空間的74%,史稱其為「克卜勒猜想」。
不過這個猜想一直沒有人能證明說對或是提出反例說錯,即便是傳奇的數學王子高斯,也只不過證明了一個特例限制下,上限是74%沒錯。所以這個猜想就一直卡住了,在1900年國際數學家大會,還被Hilbert列為23道最重要的數學問題其中之一——第18題。一直到了2014年,克卜勒猜想才被Hales證明。
最密堆積
要弄出最密堆積,先從第一層開始吧。考慮半徑為1的圓形,下圖左是像教室座位一樣整齊的排列,這個面積密度為π/4≈79%,但它並不是最密集的排列方法,因為每一張椅子旁邊只有四張椅子。下圖右才是最密堆積,每一張椅子旁邊有六張椅子,這方法的面積密度為π/2/Sqrt(3)≈91%,在1890年被Thue證明。
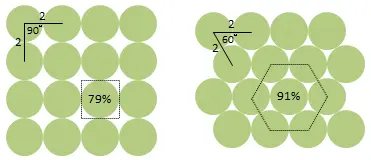
這種一格旁邊有六格鄰兵的設計,也被許多戰棋遊戲所採用。另外,雪花也是對稱的六角形結構——❄️。演唱會的椅子應該要這樣擺,空間利用率最高,而且後排的人可以從前一排二個人中間的縫隙看出去,比較不會被擋到。

接下來開始排第二層,考慮半徑為1的球體,第二層的排法也跟第一層一樣,只是第二層要向右向下各平移距離1,使得第二層球堆在第一層球與球的縫隙中,第三層如法炮製,再向右向下各平移距離1,結果如下圖,這種方法叫面心立方。
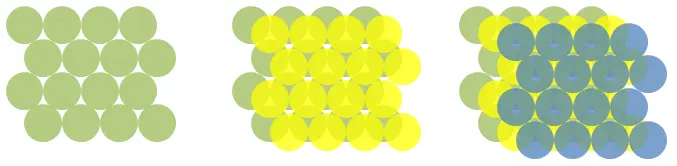
第三層也可以是第二層向左向上各平移距離1,也就是第三層在第一層正上方,這種方法叫六方晶系。
把面心立方的第一層叫A、第二層叫B、第三層叫C,那麼面心立方就是A/B/C/A/B/C/…不斷重複,而六方晶系就是A/B/A/B/…不斷重複。面心立方和六方晶系,都是球體的最密堆積,體積密度為π/3/Sqrt(2)≈74%。
自然界有許多原子的排列就是最密堆積,例如金、銀、銅是面心立方堆積,而鈹、鎂是六方晶系堆積,既然是最密的,所以常溫下多半是固體,而且是大多是作用力強的金屬。
更高維度的最密堆積
如果我們把裝球的最密堆積拓展到其他維度,這時『球』指的意思是空間中到一個固定點『球心』的距離不超過某個固定長度『半徑』,舉例來說:
| 維度 | 『球』的例子 | 最密堆積密度 |
|---|---|---|
| 一維直線 | 【球心】原點(0) 【半徑】1公尺 【方程式】x²<=1,左右1公尺內 | 1=100% |
| 二維平面 | 【球心】原點(0,0) 【半徑】1公尺 【方程式】x²+y²≤1,半徑1公尺的圓形內 | π/2/Sqrt(3)≈91% |
| 三維空間 | 【球心】原點(0,0,0) 【半徑】1公尺 【方程式】x²+y²+z²≤1,半徑1公尺的球體內 | π/3/Sqrt(2)≈74% |
| 四維時空 | 【球心】原點(0,0,0,0) 【半徑】1公尺、1秒 【方程式】x²+y²+z²+t²≤1,距今前後t≤1秒、半徑Sqrt(1-t²)公尺的時空球內 | ? |
| N維空間 | 【球心】原點(0,0,0,…,0) 【半徑】1單位 【方程式】x₁²+x₂²+x₃²+…+xₙ²≤1,半徑1單位的N維球內 | 至今只有N=1,2,3,8,24被證明出來 N=8: π⁴/384≈25% N=24: π¹²/12!≈0.2% |
我們知道一維、二維、三維空間的最密堆積方法,但不知道四維的最密堆積方法(註)。2016年Viazovska證明出八維和二十四維空間的最密堆積,因此獲得2022年的菲爾茲獎(此獎被稱為數學界的諾貝爾獎)。
註:其實數學家也有用類似的方法算出各維度的最密堆積,例如N=4~7分別為π²/16≈62%、π²/15/sqrt(2)≈47%、π³/48/sqrt(3)≈37%、π³/105≈30%,只是這些數字都還沒有被證明出來是最密的。