一言以蔽之:費米能階是電子有50%機率佔據的假想能階。
在熱力學平衡下,能階ϵ被電子占據的機率滿足Fermi-Dirac distribution f(ϵ)=1/(1+exp((ϵ-Ef)/(k*T))),當ϵ=Ef(Fermi Level)時,f(ϵ)=50%,電子有50%機率佔據。
對於半導體來說,費米能階會落在conduction band和valence band的中間。
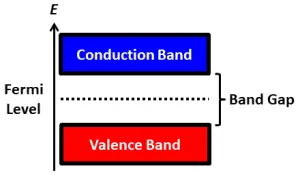
我們知道,如果在純的半導體,故意摻入雜質,就可以改變自由電子、電洞濃度,也就是會改變費米能階的位置。如果是n-doped,那麼Fermi Level會上升;如果是p-doped,那麼Fermi Level會下降。就拿這題常考題來當例子說明吧。
計算矽在下列條件下的費米能階Ef相對於本質費米能階Efi的位置: (a) T=300K, Nd=3e16cm⁻³, Na=0cm⁻³ (b) T=300K, Nd=1e15cm⁻³, Na=4e15cm⁻³ (c) T=300K, Nd=Na=2e15cm⁻³
從上次計算的結果繼續,本題答案如下:
T=300K之下,Si的nᵢ=1.5e10cm⁻³ (a) 電子濃度n=3e16,電洞濃度p=7.5e3,代入 Ef-Efi=k*T*ln(n/nᵢ)=0.026*ln(3e16/1.5e10)=0.38eV Efi-Ef=k*T*ln(p/nᵢ)=0.026*ln(7.5e3/1.5e10)=-0.38eV 二式都得到一樣的答案,Ef比Efi高0.38eV,因為n-doped會使Fermi Level上升 (b) 電子濃度n=7.5e4、電洞濃度p=3e15,代入 Ef-Efi=k*T*ln(n/nᵢ)=0.026*ln(7.5e4/1.5e10)=-0.32eV Efi-Ef=k*T*ln(p/nᵢ)=0.026*ln(3e15/1.5e10)=0.32eV 二式都得到一樣的答案,Ef比Efi低0.32eV,因為p-doped會使Fermi Level下降 (c) 電子濃度n=1.5e10、電洞濃度p=1.5e10,代入 可得Ef-Efi=0eV 因為n=p,等效就是intrinsic Si,Fermi Level就會跟intrinsic Fermi Level一樣