一言以蔽之:半導體能隙就是價帶頂端至導帶底端的差異。
今天有大學生問我了一題半導體物理的習題:
計算矽在下列條件下的熱平衡電子與電洞濃度: (a) T=300K, Nd=3e16cm⁻³, Na=0cm⁻³ (b) T=300K, Nd=1e15cm⁻³, Na=4e15cm⁻³ (c) T=300K, Nd=Na=2e15cm⁻³ 如果材料換成砷化鎵,重新計算(a)(b)(c)。
考慮純的矽instrinsic Si,其在有溫度的情況下,因為熱能可以讓共價鍵會被破壞,因此就有電子可以被釋放出來,變成電子電洞對,在熱平衡的情況下,電子濃度n=電洞濃度p=本質半導體電洞電子濃度nᵢ。
然而在常溫下,nᵢ這個數字太小,以T=300K的Si來說,nᵢ只有1.5e10cm⁻³,不太導電,所以矽只能叫「半」導體而不是導體。那怎麼辦呢?就是doping,故意將雜質摻入純的半導體,摻入施體donor濃度Nd會增加電子濃度、摻入受體acceptor濃度Na會增加電洞濃度,如果同時摻入和Nd和Na就會互相抵消。而經摻雜後的半導體之電子濃度n、電洞濃度p,會滿足n*p=nᵢ²。
所以這題常考題的答案如下:
T=300K之下,Si的nᵢ=1.5e10cm⁻³ (a) 電子濃度n=Nd-Na=3e16,電洞濃度p=nᵢ²/n=(1.5e10)²/3e16=7.5e3cm⁻³ (b) 電洞濃度p=Na-Nd=3e15,電子濃度n=nᵢ²/p=(1.5e10)²/3e15=7.5e4cm⁻³ (c) Nd和Na互相抵消,所以電子濃度n=電洞濃度p=nᵢ=1.5e10cm⁻³
如果把矽換成砷化鎵,這題的答案為:
T=300K之下,GaAs的nᵢ=1.8e6cm⁻³ (a) 電子濃度n=Nd-Na=3e16,電洞濃度p=nᵢ²/n=(1.8e6)²/3e16≈0cm⁻³ (b) 電洞濃度p=Na-Nd=3e15,電子濃度n=nᵢ²/p=(1.8e6)²/3e15≈0cm⁻³ (c) Nd和Na互相抵消,所以電子濃度n=電洞濃度p=nᵢ=1.8e6cm⁻³
本質半導體內的自由電子與電洞濃度nᵢ,隨著溫度上升而變大,nᵢ∝T^(3/2)exp(-Eg/2kT),其中這個Eg叫做能隙energy gap,就是價帶頂端至導帶底端的差異,所以也叫帶隙band gap。
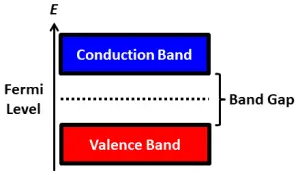
導體的Eg=0,而絕緣體的Eg很大,半導體就介於導體和絕緣體之間,舉例來說,Si的Eg=1.12eV、GaAs的Eg=1.42eV、GaN的Eg=3.4eV。
如果把半導體產業分成三個階段,第一代半導體材料為Si,第二代半導體材料為GaAs,都已經被廣泛地使用,而近年來新流行的是第三代半導體材料,也就是寬能隙(Eg比較大)的半導體,包括SiC、GaN等等。
最後,提一下bandgap在類比電路中的使用,全名其實叫bandgap voltage reference,不過大家都已經習慣簡稱它為bandgap。無論電源、溫度、製程如何變化,這個電路都可以產生一個固定的參考電壓約1.2V(大致是Si Eg≈1.2eV)。