一言以蔽之:MECE原則是一種好用的分析問題邏輯方法。
科技公司裡明明有許多學歷優秀的員工,但這些人寫出來的投影片往往漏東漏西,根據顧問公司的研究,這是因為他們的思考缺乏系統邏輯性,造成寫出來的報告就經常是片面的。如果我們採用MECE的思考原則,就可以得到更完整資訊,這樣的報告,可以讓其他人更容易理解和吸收。
所謂MECE(mutually exclusive, collectively exhaustive),讀作「me-see、米西」,是1960年代由麥肯錫公司提出的邏輯分析法。
考慮一個母集合U,其有三個子集合A,B,C,滿足:
A∩B=∅
B∩C=∅
C∩A=∅
A∪B∪C=U
其中∩是交集、∪是聯集、∅是空集合。
那麼A,B,C就滿足「mutually exclusive, collectively exhaustive」。
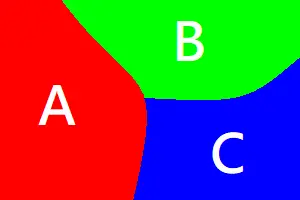
這意思是說,有一塊電路U,可以分成三個子電路A,B,C,U=A+B+C,而A,B,C兩兩之間完全不相干。今天電路U有一個bug,我們不知道bug在哪裡,但我們已經驗證出子電路A沒有bug、子電路B也沒有bug,那麼就可以推論出bug必然在子電路C裡面。
如果我們可以把一個複雜的大問題(母集合整體)拆分成許多獨立的小問題(子集合),就可以一一地分析小問題。就像剝洋蔥一樣,可以一層一層地更好理解問題的核心。這種不重疊、不遺漏的分類,就叫做MECE。其中ME的意思就是彼此獨立、相互排斥,CE的意思就是互無遺漏、完全窮盡。
在解決問題時,如果能使用MECE原則,就會條理清楚,可以用有邏輯的方式,來思考模糊的大問題。許多問題解決高手其實就是把MECE內化成其反射性思考,和他們討論問題,就會發覺他們的邏輯思路很清晰。
事實上,培養邏輯思維遠比學習專業技能難多了,要將MECE內化到日常生活中是很不簡單的。比如說我們在填寫一些問卷時,其中一個題目是問年齡:10~20歲、20~30歲、30~40歲。那如果『恰好』20歲的人到底是要選10~20歲還是20~30歲呢?另外是41歲的人要選什麼呢?這例子就是犯了選項沒有互斥且窮盡的錯,更為正確的選項是≤9歲、10~19歲、20~29歲、30~39歲、≥40歲。
假設我們無法拆分到子集合是互相獨立的,那麼De Morgan’s Law就可以派上用場了,這是集合論中一個很重要的定理。
(A∪B)ᶜ=Aᶜ∩Bᶜ
(A∩B)ᶜ=Aᶜ∪Bᶜ
其中Aᶜ、Bᶜ分別是A的差集、B的差集(complement)。
第一條式子是說,有一塊電路是A和B合起來的,現在驗證出這塊電路沒有bug,那麼表示bug一定不在A也不在B。第二條式子是說,已經驗證出電路A和電路B共用的那塊電路沒有bug,那麼表示bug會在A的外部或B的外部。第一條式子比第二條式子更常用,因為可以把bug聚焦在較小的區域。