一言以蔽之:二進位是效率最高的進位制度。
之前的文章,我們提到八卦和六十四卦,並用3-bit和6-bit的binary number system來理解,但這其實把歷史顛倒了,因為二進位這個發想,一個很重要的源頭就是六十四卦圖。
有個軼聞是,發明微積分的萊布尼茲在研究完康熙時代的六十四卦圖後,寫了一篇二進位算術體系的論文,結果投稿被審查委員打槍,期刊的editor當時說這binary system沒用。一直到了電腦問世後,二進位的重要性才顯示出來。
我們現在用bit來表示0,1,是從binary digit來的,取出binary的bi-(bi-字根是雙的意思),從digit取出t,就創造出bit這個字。
因為人類有十根手指頭,所以許多古代文明都發展出十進位,包括中國、印度、埃及、希臘……等,流傳至今的符號則有漢字(中國)的一二三十百千、阿拉伯(印度)的的12345、羅馬(希臘)的ⅠⅡⅢⅤⅩ。
少數不是十進位的文明有瑪雅以及巴比倫,瑪雅文明使用二十進位,巴比倫文明使用六十進位。其中蘇美人開始使用、傳至巴比倫的六十進位,由於巴比倫有楔形文字,所以也流傳到現代了,我們現在仍然使用六十進位於時間和角度。古人為什麼選24、60、360(一小時60分鐘、一天24小時,一個圓360°),是因為這些數字的因數最多,分解以後仍然是整數,例如一小時分成四刻鐘,每刻鐘是15分鐘。所以撲克牌遊戲24點也是類似的原因。
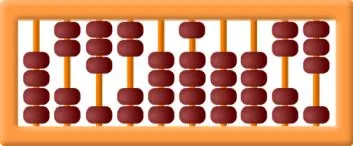
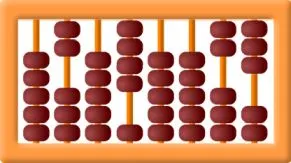
由於電腦的關係,我們現在已經習慣二進位了,但為什麼當年設計電腦時選二進位呢?這是因為二進位的效率高。什麼叫效率高呢?上面二個圖分別是十排的五進位算盤、八排的六進位算盤,這二個算盤有一樣多的(四十顆)珠子,哪一個算盤能夠表示的數字範圍大,就是效率高。由下列的計算可以知道,十排的五進位算盤效率比八排的六進位算盤來得高。
- 十排的五進位算盤:最小數字是0,最大數字是4*(5^0+5^1+5^2+…+5^9)=9765624。
- 八排的六進位算盤:最小數字是0,最大數字是5*(6^0+6^1+6^2+…+6^7)=1679615。
考慮有N顆珠子的算盤,使用n進位,會有(N/(n-1))排,這個(N/(n-1))排的n進位算盤,最小數字是0,最大數字是(n-1)*(n^0+n^1+n^2+…+n^(N/(n-1)-1)=n^(N/(n-1))-1,其中N是正整數常數,n是大於等於2的正整數。
要求n^(N/(n-1))-1的極值,就是求ln[n^(N/(n-1))]=N*ln(n)/(n-1)的極值(因為對數是單調遞增函數),也就是求ln(n)/(n-1)的極值,可以得到這函數在n=2有最大值。因此,二進位是效率最高的進位制度。